C01 Computational theory for complex dynamics and its applications
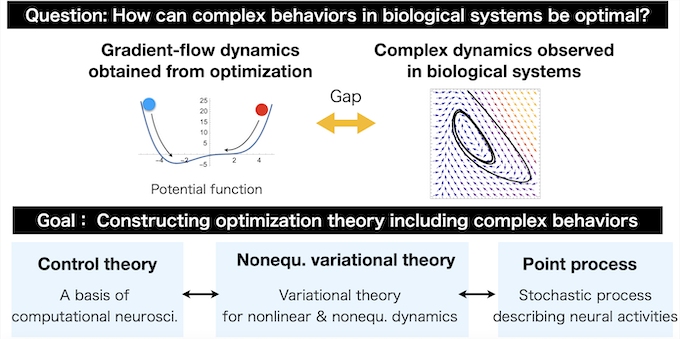
In elucidating the optimality and functionality of biological information processing, including those of the brain, optimization theories such as estimation, control, and learning developed in engineering are essential. These theories typically result in optimal dynamics that manifest as gradient flows descending a potential function due to their property of minimizing an objective function. However, when we observe actual biological information processing, many phenomena display more complex dynamical behaviors, such as oscillations or chaos, making the theoretical relationship between these complex dynamics and optimization theories unclear. Simultaneously, in engineering, the efficacy of algorithms incorporating factors like inertia has been empirically confirmed, which do not always conform to gradient flow structure.
This research seeks to advance a theory that broadens the concept of generalized gradient flows and to elucidate its relation to theories of estimation and control, thereby investigating the computational significance that complex biological dynamics contribute to biological information processing.
The concept of generalized gradient and nonequilibrium flows was introduced in our recent work on establishing thermodynamic theories for equilibrium and non-equilibrium chemical reaction systems, clarifying their information geometric structure. Generalized nonequilibrium flows, an extension of generalized gradient flows, include any chemical reaction systems obeying mass action kinetics, thus encompassing complex dynamics such as chaos. They also have a correspondence with Bayesian filters and can be regarded as an information geometric generalization of the recent L2-Wasserstein theory.
In this study, we will extend this theoretical framework to clarify the relationship between complex dynamics and information processing. Specifically, we will address two main problems: For the first problem, we attempt to describe optimization dynamics that include inertia (generalized momentum) by extending non-equilibrium variational theory; For the second task, we aim to link our theory to point processes via large deviation theory, providing methodologies for interpreting and analyzing neuronal firing models and experimental data.

Principal investigator: Tetsuya Kobayashi
Professor, Institute of Industrial Science, The University of Tokyo
