C01 複雑ダイナミクスを内包しうる計算原理理論の構築と応用
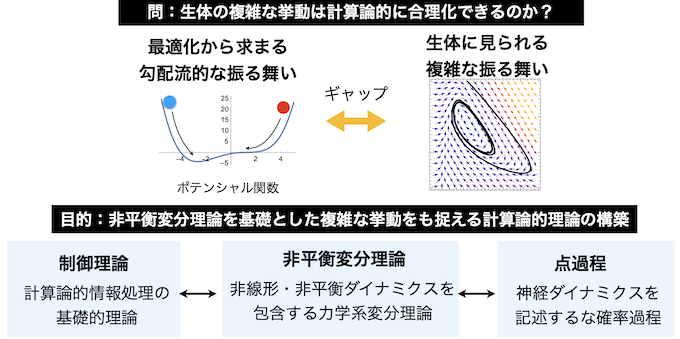
脳をはじめとした生体情報処理の最適性や機能性を解明する上で、推定理論・制御理論・学習理論などの工学分野で発展した最適化理論は不可欠です。目的関数を最小化するという理論の性質から、これらの理論が導く最適ダイナミクスは一般にポテンシャル関数を下る勾配流型になります。しかし現実の生体情報処理現象に目を向けると、その多くは振動やカオス的振る舞いなどより複雑で多様な動的挙動をも示し、これら複雑ダイナミクスと最適化理論との関係は理論的に明らかではありません。また同時に、工学的な最適化の現場や実際の運用においても、勾配流的な振る舞いに慣性などを加えて拡張し、勾配流には必ずしも一致しないアルゴリズムの有効性などが経験的に確認されています。
本研究は、一般化勾配流を拡張した理論を発展させ、その推定理論・制御理論との対応を明らかにすることで、複雑な生体ダイナミクスが生体情報処理にもたらす計算論的意義を探求します。
一般化勾配流・一般化流の概念は、近年我々が平衡・非平衡化学反応系の熱力学理論を構築する過程で導入し、その情報幾何学的構造を明らかにしたものです。一般化勾配流の拡張である一般化流は任意の質量作用に従う化学反応系を包含し、したがってカオスなどの複雑ダイナミクスをその射程に含みます。また情報学のベイズフィルターとの対応も持ち、近年のL2-Wasserstein理論の情報幾何学的一般化とも見ませます。
本研究ではこの、複雑なダイナミクスの情報論的性質の関連を明らかにする上で最適な枠組みを発展させます。具体的に以下の2つの課題に取り組みます。1つ目は、最適制御を取り込む形で「非平衡変分理論」を拡張すること、2つ目は 大偏差理論を介して「非平衡変分理論」と点過程とをつなぐことです。1つ目の課題では理論の最適制御への拡張を行うことで慣性(一般化運動量)を含む最適化ダイナミクスを捉えることを試みます。また2つ目の課題を介して、本理論を点過程と対応付け、神経発火モデルや神経発火実験データを解釈・解析する方法論へとつなげます。